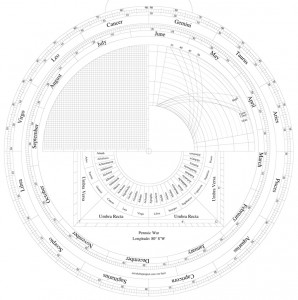
The next step in drafting the astrolabe is constructing the calendar scale.
Up until now the process of creating scales has been straightforward. The time scale on the front and the altitude and zodiac scales on the back are simple in concept and execution, requiring no math to draw. The calendar scale, on the other hand, needs to be aligned to the zodiac scale so that when the alidade pointer is rotated to a given date, the pointer crosses the zodiac scale at the Sun’s ecliptic position on that date. This is not straightforward, as the Earth’s orbit is elliptical, and the Sun appears to move along the ecliptic at different speeds at different times of the year; in other words, it covers a slightly wider arc per day in winter than in summer.
Traditionally, there are two ways to allow for the Sun’s uneven motion. The first is the concentric method, where the calendar circles are drawn concentrically with the zodiac circles. In this case the days are drawn on the scale so that the space between the day marks varies depending on where on the scale they are. To accomplish this, the astrolabe maker must determine the exact location of the Sun for each day. This method requires a lot of careful calculation and measurement, and would be very time-consuming, unless reference tables are available. I could use this method, as I have access to an accurate ephemeris. But the drawing of the day lines would be more finicky that I would like to attempt for a first try.
The second, simpler method is the one I’m going to use. This second method, the eccentric method, offsets the center of the calendar scale from the center of the zodiac scale, modeling the offset of Earth’s orbit. This method is actually very accurate, well within the overall accuracy of the astrolabe itself [Morrison: 111] and was used extensively by astrolabe makers. To accomplish the drafting this scale accurately, three factors must be known in advance: The direction of the offset, the distance of the offset, and the rotation of the calendar.
First, direction; from Stoeffler:
“Find the Apogee of the Sun, corresponding to the time of construction of our astrolabe through the Alfonsine Tables, or through other tables. For example, in the Year of Christ 1510, with exact calculations, it is around 1 degree 16 minutes of Cancer. Therefore, get ready to place it on this point of Cancer, as this is its position in the year mentioned, that is, at the 16th minute of the second degree of Cancer.” [Stoeffler: 66]
The Alfonsine Tables {http://en.wikipedia.org/wiki/Alfonsine_tables} and other tables mentioned are tables of astronomical data that would have been expected to be available to someone designing astronomical instruments of the period.
Lacking such tables, I will have to do some computation. Morrison goes deeply into the math in his section on drawing the eccentric calendar; so I won’t try to duplicate his work in detail here, if you are interested I recommend his book very much. Here is a summary of the process:
Step 1. Compute the Julian Century (T)
The Julian Day for January 1, 2000 at noon UT is 2451545.0 [after Morrison: 337].
The current Julian Day (For the time of writing (November 14, 2011), is 2455879.5).
The Julian Century is computed as follows:
T = (2455879.5 – 2451545.0) / 36525 = 0.118672142 [after Morrison: 337].
Step 2. Find the angle of perihelion (Q)
Q = 102.937348 + (1.7195269*T) + (0.00045962*T^2) + (0.000000499*T^3) = 103.1414144 [after Morrison: 112].
Or 103 degrees rounded off. Counting around counterclockwise from Aries 0, this gives me an angle of Cancer 13.
Next, I need to know the magnitude of the offset. Stoeffler gives an offset of 1/32nd of the inner radius of the zodiac ring (0.03125 x R) [Stoeffler: 67]; where Morrison computes it to be 0.0334 x R [Morrison: 112]. Morrison is definitely the more accurate; but as the difference is about a hundredth of an inch for the circle I’ll be drawing, I’ll go with Stoeffler, as it is easier to draft.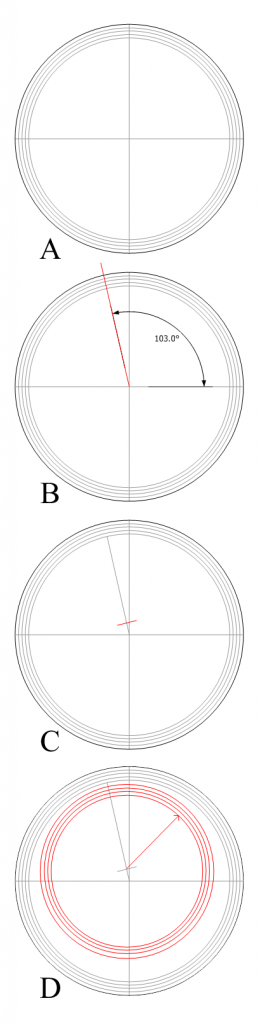
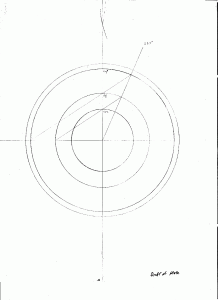
With these first two factors known I can draw the rings for the calendar. The procedure is as follows (See the figure to the right):
A. Find the center of the zodiac ring. This is, of course already marked; I used it to draw the zodiac circles.
B. Draw a construction line (to be erased later) from the center to the inside edge of the zodiac ring at an angle of 103 degrees from Aries 0 (to Cancer 13).
C. Divide this line repeatedly until you have a mark 1/32 of the way from the center to the edge (exaggerated here).
D. Using that point as a center, draw the circles for the calendar ring.
Finally, I need to know where to start drawing the calendar; that is, how to rotate the calendar so that it is properly aligned with the zodiac.
Stoeffler calls for aligning the beginning of January with Capricorn 20:
“Make the subdivisions of the days and of the months in this way. Set the rule on the center E and on the 20th degree of Capricorn and draw a line segment crossing all the eccentric circles. It will point out the beginning of January and be marked with a G. Starting from it, in the opposite direction to the succession of the Signs, count around 5 degrees 20 minutes. Set the rule between this point and the center E. Draw a line from the first eccentric circle to the second, which will be H. The remaining arc must now be divided (this small arc excepted) into 360 equal parts…” [Stoeffler: 67]
The sky has shifted a bit in 500 years. Using the equations in Morrison’s book, I come up with a rotation figure of -79.4757 (call it -79.5 degrees). Starting from Aries 0 and counting clockwise (remember, the sun moves counterclockwise through the zodiac ring, and we are rotating backwards) that puts the line for the beginning of January at Capricorn 10.5.
I now have all the figures I need to begin drafting the Calendar Ring.