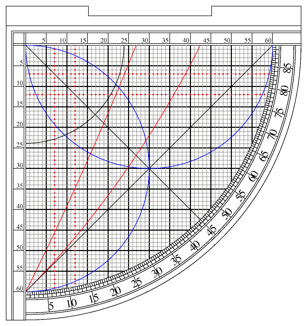
Deconstructing the Sine Quadrant-Part 1: Introduction
- on 01.26.14
- Random Jottings, Sine Quadrant
- Comments Off on Deconstructing the Sine Quadrant-Part 1: Introduction
The development of mathematics and the sciences through-out the medieval period spawned a range of clever, elegant tools for observation and computation. Devices such as the Armillary Sphere and the Astrolabe are familiar sights in the art of both Europe and the Middle East; but lesser known are a class of tools known as quadrants.
Quadrants come in several different varieties, each with their own uses. Astrolabe Quadrants “fold up” the lines and scales of an astrolabe into a compact device that can perform most of the same calculations. Horary Quadrants deal with telling time and converting between differing time keeping systems. The subject I will be discussing in this current series is a third type, the Sine Quadrant, also known as a Sinecal or Rubul Mujayyab, a device that allows the user to perform quick, accurate trigonometric calculations, along with several other related functions.
(Here [SineQuadrant.pdf] is a link to a PDF of a typical sine quadrant that you can print out and use to follow the discussion)
The Basic Features:
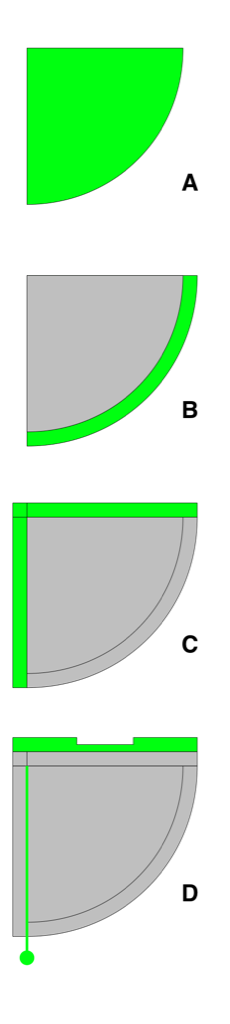
Most quadrants are shaped, logically enough, as a quarter-circle, with two straight sides meeting at a right angle and a quarter-circle arc closing the open end (A).
The Angle Scale
Along the curved side is a scale marked off in 90 degrees, usually grouped into five degree sections. Used with the sights and a weighted cord (see below), the user can sight on a target and determine the angle of elevation by seeing where the weighted cord lies on the angle scale (B).
The Horizontal and Vertical Scales
Along each straight edge of the sine quadrant is a scale. These are traditionally divided into 60 units and subdivided into 12 five-unit sections. This base-60 (or sexagesimal) numbering is a hold-over from the ancient Babylonian number system that still survives in our divisions of time and angles. The horizontal scale is used for computing the Sine of an angle, the vertical scale is used to compute the Cosine of an angle (C).
The Cord
At the right-angle of the quadrant there is a small hole from which hangs a weighted cord. This cord is used as an index line when doing calculations. It also works as a plumb line when the quadrant is used to measure altitudes.
The Sights
On most quadrants there is also a set of sights. Sometimes these are sighting vanes with holes for sighting through; sometimes a square notch is cut out of one side, providing two posts that can be sighted across (D).
The Sine/Cosine Grid
On the face of the sine quadrant there is a grid (60 by 60) matching the horizontal and vertical scales dicussed above. As on the scales, every fifth line is often set apart, either by width or with special markings.
Measuring angles
The most basic function of the Sine Quadrant, common to all quadrants, is measuring angles. By using the sights, the weighted cord, and the angle scale together, a user can determine a vertical angle with a good amount of accuracy.
Finding the Sine and Cosine of an Angle
It is often necessary to find the Sine or Cosine of an angle when performing a calculation. Finding the rough figure for Sine or Cosine given an angle is easy using a Sine Quadrant.
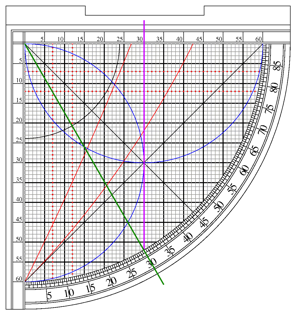
For example: Given the angle of 30 degrees, find the sine.
— Holding the quadrant, move the cord until it is held taught on the 30 degree mark (Green line).
— Next look at the point that the cord crosses the curved edge do the grid.
— Follow that point vertically until you reach the horizontal sine scale and read the result (Purple Line). An angle of 30 degrees gives us the correct sine of 30/60 or 0.5.
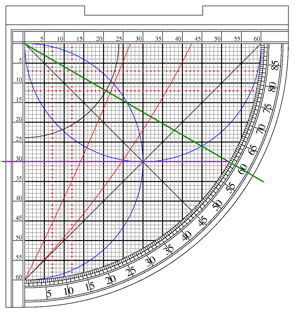
Computing Cosine is done in a similar manner. Notice that as the cord is rotated from 0 to 90 degrees the sine varies from 0/60 (0) to 60/60 (1) with the Cosine changing in reverse from 1 to 0, as expected.
To find the angle represented by a sine, the process works in reverse: Given a sine of .5 or 30/60, trace the 30 line down to the rim of the grid, place the cord there and read the angle.
In the next post I will dig into some of those advanced lines and functions you can see on the face of the sine quadrant.
Sources:
Top photo: Gerry Young, released under Creative Commons Attribution Share-alike 3.0 license (http://en.wikipedia.org/wiki/File:Taking_the_Measure.JPG)